Some Fun with GNUPLOT

Introduction

This page contains a couple of cool graphs done with GNUPLOT. GNUPLOT is great and free! GNUPLOT is available for download here.

The GNUPLOT commands used to generate each graph are listed after each figure. Note that in a couple of cases the formula lines are very long. This is indicated with backslash ("\") characters. In GNUPLOT, the backslash means that the following line is a continuation of the current one. You must either enter the commands exactly as shown (with the "\" followed by a new line) or combine them into a single line omitting the "\" characters.

Gif files were produced with the following commands: 

set terminal gif
set output "out.gif"
replot
I.e., if you type in the GNUPLOT commands and can see the a figure on your screen, these commands will save the image as a .gif file.

My home page.





Sphere 


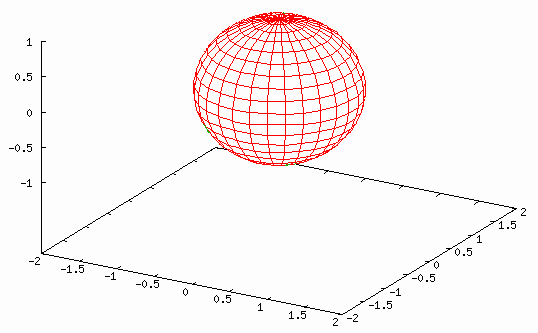
set nokey
set parametric
set hidden3d
set view 60
set isosamples 30,20
set xrange[-2 : 2]
set yrange[-2 : 2]
set zrange[-1 : 1]
splot [-pi:pi][-pi/2:pi/2] cos(u)*cos(v), sin(u)*cos(v), sin(v)




Torus 


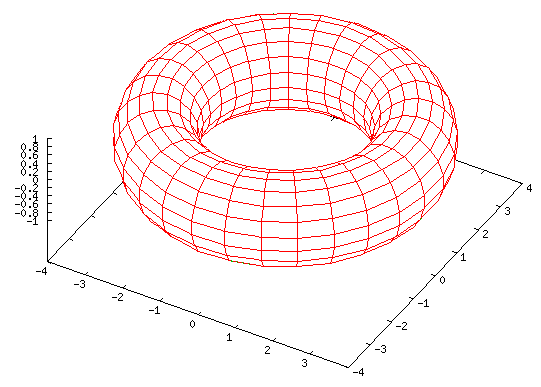
set nokey
set parametric
set hidden3d
set view 30
set isosamples 30,20
splot [-pi:pi][-pi:pi] cos(u)*(cos(v)+3), sin(u)*(cos(v)+3), sin(v)




Spiral 


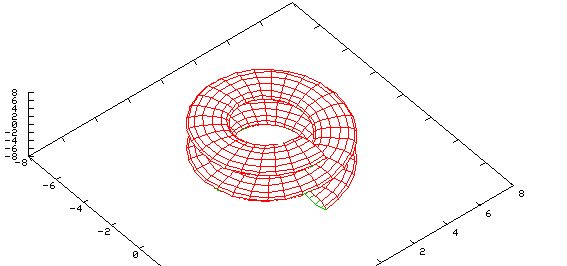
set nokey
set parametric
set hidden3d
set view 15,50
set isosamples 60,15
set xrange [-8:8]
set yrange [-8:8]
set zrange [-8:8]
set ticslevel 0
splot [-2*pi:2*pi][-pi:pi] cos(u)*(cos(v)+3), sin(u)*(cos(v)+3), sin(v)+u

A side view...


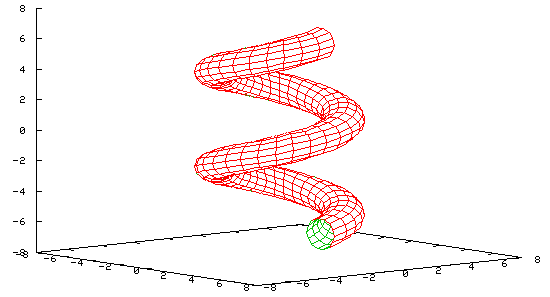
set nokey
set parametric
set hidden3d
set view 80,50
set isosamples 60,15
set xrange [-8:8]
set yrange [-8:8]
set zrange [-8:8]
set ticslevel 0
splot [-2*pi:2*pi][-pi:pi] cos(u)*(cos(v)+3), sin(u)*(cos(v)+3), sin(v)+u




Conic Spiral - Nautilus 


set nokey
set parametric
set hidden3d
set view 65,330
set isosamples 60,20
splot [0:3*pi][-pi:pi] u*cos(u)*(cos(v)+1), u*sin(u)*(cos(v)+1), u*sin(v)

A top-down view...


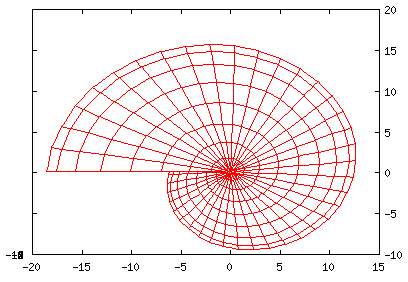
set nokey
set parametric
set hidden3d
set view 0,0
set isosamples 60,20
splot [0:3*pi][-pi:pi] u*cos(u)*(cos(v)+1), u*sin(u)*(cos(v)+1), u*sin(v)




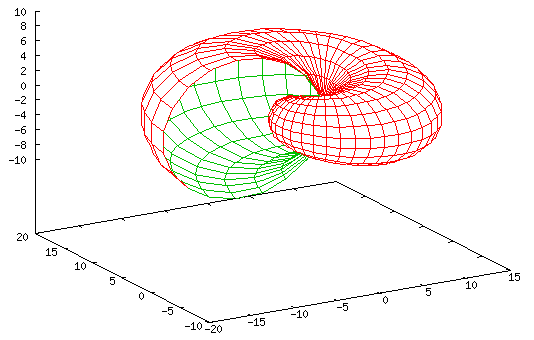
Conic Spiral - Toroid Consuming Own Tail 


set nokey
set parametric
set hidden3d
set view 65,340
set isosamples 60,20
splot [0:3*pi][-pi:pi] cos(u)*(u/(3*pi)*cos(v)+2),\
sin(u)*(u/(3*pi)*cos(v)+2), u*sin(v)/(3*pi)

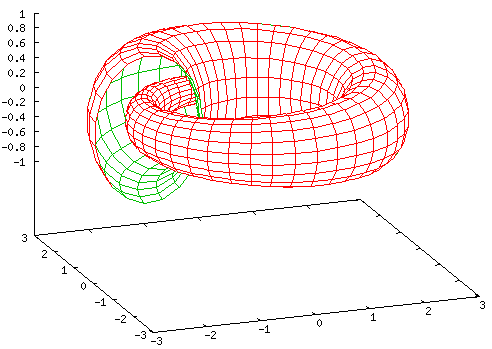
A top-down view...


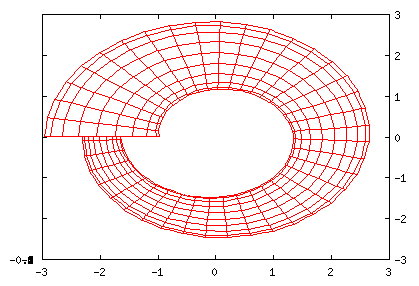
set nokey
set parametric
set hidden3d
set view 0,0
set isosamples 60,20
splot [0:3*pi][-pi:pi] cos(u)*(u/(3*pi)*cos(v)+2),\
sin(u)*(u/(3*pi)*cos(v)+2), u*sin(v)/(3*pi)




Sea Shell 


set nokey
set noborder
set noxtics
set noytics
set noztics
set parametric
set hidden3d
set view 90,330,1,1.3
set isosamples 300,20
splot [0:13*pi][-pi:pi] u*cos(u)*(cos(v)+1), u*sin(u)*(cos(v)+1), \
u*sin(v) - ((u+3)/8*pi)**2 - 20




Trefoil Knot 


set nokey
set parametric
set hidden3d
set view 60,0
set isosamples 60,15
splot [-2*pi:2*pi][-pi:pi] cos(u)*cos(v) + 3*cos(u)*(1.5+sin(1.5*u)/2),\
sin(u)*cos(v) + 3*sin(u)*(1.5+sin(1.5*u)/2), sin(v)+2*cos(1.5*u)

A top-down view...


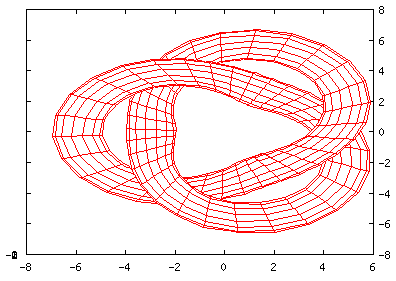
set nokey
set parametric
set hidden3d
set view 0,0
set isosamples 60,15
splot [-2*pi:2*pi][-pi:pi] cos(u)*cos(v) + 3*cos(u)*(1.5+sin(1.5*u)/2),\
sin(u)*cos(v) + 3*sin(u)*(1.5+sin(1.5*u)/2), sin(v)+2*cos(1.5*u)




Higher-Order Knot 


set nokey
set parametric
set hidden3d
set view 30,40
set isosamples 200,15
splot [-3*pi:3*pi][-pi:pi] cos(u)*cos(v)+3*cos(u)*(1.5+sin(u*5/3)/2),\
sin(u)*cos(v)+3*sin(u)*(1.5+sin(u*5/3)/2), sin(v)+2*cos(u*5/3)

A top-down view...


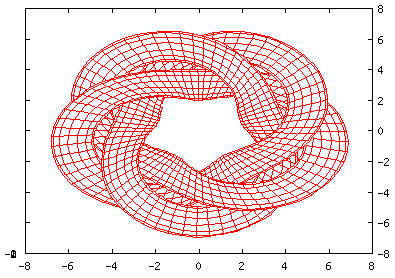
set nokey
set parametric
set hidden3d
set view 0,0
set isosamples 200,15
splot [-3*pi:3*pi][-pi:pi] cos(u)*cos(v)+3*cos(u)*(1.5+sin(u*5/3)/2),\
sin(u)*cos(v)+3*sin(u)*(1.5+sin(u*5/3)/2), sin(v)+2*cos(u*5/3)




Dini's Surface

Dini's surface has a constant negative curvature (a sphere has a constant positive curvature). It is constructed by twisting a pseudosphere.

Mostly, this surface is here because it looks pretty.


set nokey
set parametric
set hidden3d
set noautoscale
set view 70, 20, 7
set isosamples 40,20
splot [0:4*pi][0.001:2] cos(u)*sin(v), sin(u)*sin(v), \
cos(v)+log(tan(v/2))+0.2*u -4




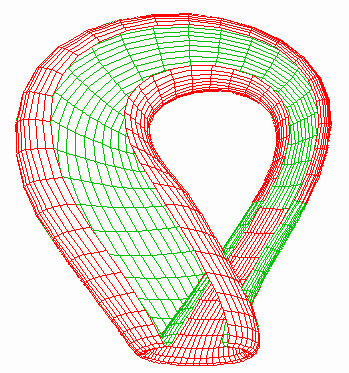
Mobius Surface

The Mobius surface (or Mobius "Strip") is a one-sided object, with only one edge. It may appear at first glance to have two sides, however it is possible for one to walk from one side to the other without having to cross the edge - because of the twist.


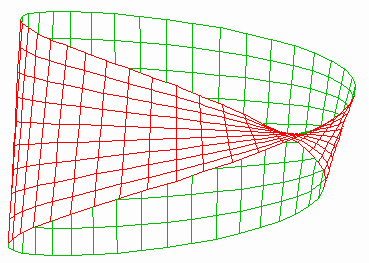
set nokey
set noborder
set noxtics
set noytics
set noztics
set parametric
set hidden
set isosamples 40,10
set view 90, 45
splot [0:2*pi][-.1:.1] cos(u) + v*cos(u/2) * cos(u), \
sin(u)+v*cos(u/2)*sin(u), v*sin(u/2)

Another view...


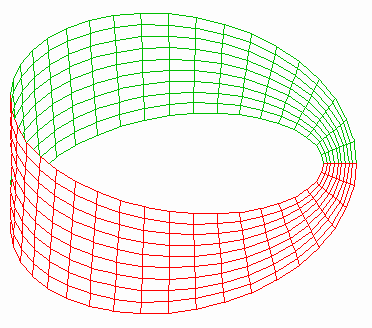
set nokey
set noborder
set noxtics
set noytics
set noztics
set parametric
set hidden
set isosamples 40,10
set view 30, 0
splot [0:2*pi][-.1:.1] cos(u) + v*cos(u/2) * cos(u), \
sin(u)+v*cos(u/2)*sin(u), v*sin(u/2)




Klein Bottle

The Klein bottle, similar to the Mobius surface above, is one-sided; however unlike the Mobius surface, it has no edges. One way to think of it, is as two Mobius strips joined at their edges (the corollary is that if you cut a Klein Bottle in half along its length you get two Mobius strips).

A Klein bottle can only really exist in four (or higher) dimentions; in three dimensions the neck of the bottle bends around and must pierce the side of the bottle. In four dimentions the klein bottle does not intersect itself. So what you see below is really a three-dimensional immersion of a four-dimentional object (although it's really a two-dimensional projection of a three dimensional immersion...).

Think of a regular wine bottle with a cork - if you are outside, you cannot get inside without getting past the cork. A bottle is topologically isomorphic to a disc - there's a top and a bottom, separated by an edge. The cork serves the function of blocking the edge of the bottle.

If one were to stick a cork in the neck of a Klein bottle (in the bottom of the figure below), it is still possible to get inside without having to get past the cork. One simply follows the side of the bottle up, around, down to the neck, and through the side, to end-up inside the bottle without ever having to squeeze past the cork. You would have to (along with the neck) squeeze through the side of the bottle without breaking it, but in four dimensions this is easy to do.

A fun site with lots of information, and with real three-dimensional immersions of Klein bottles for sale is available here. A more mathematically rigorous site appears here. (Note that I am not associated with either of these two sites.) 


set nokey
set noborder
set noxtics
set noytics
set noztics
set parametric
set hidden
set isosamples 40,40
set view 0, 0, 2
set xrange [-25:25]
set yrange [-25:25]
set zrange [-25:25]

#set urange [0 : pi]
set urange [0 : 2*pi]
set vrange [0 : 2*pi]

# switch function:
# 0 for x < a
# 1 for x > a
##switch(x, a) = (erf(x-a)+1)/2
switch(x, a) = (x > a ? 1 : 0)
sw(x) = switch(x - pi)

# cross-over function:
# a for x < c
# b for x > c
cross(a, b, c, x) = a * (1 - switch(x, c)) + b * switch(x, c)
cr(x) = cross(cos(x), 1, pi, x)

splot \
   6*cos(u)*(1+sin(u)) + 4*(1-cos(u)/2)*cr(u)*cos(v+pi*sw(u)), \
   16*sin(u) + 4*(1-cos(u)/2)*sin(u)*cos(v)*(1-sw(u)), \
   4*(1-cos(u)/2) * sin(v) \

"Figure-8" parameterisation...

This Klein surface can be constructed by rotating a figure eight about its axis while inserting a twist in it. This results in the figure appearing below. While (in four dimensions) this is topologically isomorphic to the Klein bottle above it's not as aesthetically appealing as the previous figure.


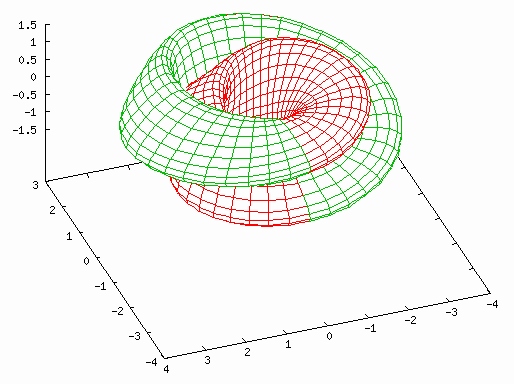
set nokey
set parametric
set hidden
set isosamples 40,40
set view 40, 250
a = 2.0
set urange [-pi/1 : 1*pi/1]
set vrange [ 0 : 2*pi]
splot \
   (a+cos(u/2)*sin(v)-sin(u/2)*sin(2*v))*cos(u), \
   (a+cos(u/2)*sin(v)-sin(u/2)*sin(2*v))*sin(u), \
   sin(u/2)*sin(v) + cos(u/2)*sin(2*v)

Three other views...




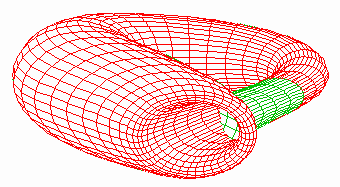
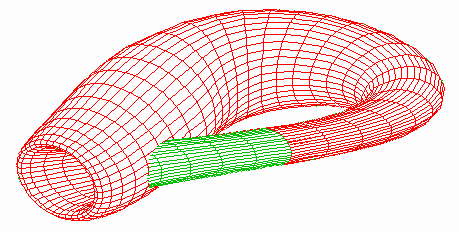
A "Cut-Away" view

Part of the side of the klein bottle has been removed so the "inside" is visible.